1 引言

地下水流系统理论是当代水文地质学的核心理论之一，是研究盆地或区域尺度地下水循环规律的有效工具(陈梦熊，2002；周仰效，2009；张人权等，2011；孙厚云，2018)。分析不同因素对地下水流系统形成演化的影响，是地下水流系统理论研究的基本内容(Freeze et al., 1967；Winter，1999；Haitjema et al., 2005；Gleeson et al., 2008；张俊等，2017；罗杰等，2020)。Tóth通过建立理想剖面二维盆地模型，讨论了均质情况下地形、盆地斜率和盆地深度等因素影响对地下水流系统的影响(Tóth，1963；Tóth，1999)。含水层非均质对地下水流系统影响显著，是控制地下水流模式的重要因素。目前，含水层非均质性对水流系统影响的探讨主要限于概念模型下的理论探讨，且多以非均质性的结构性特征为主，即假定渗透系数在空间确定的、有规律地分布(Jiang et al，2011)，如Freeze和Witherspoon(1967)讨论了简单层状非均质的情况，蒋小伟等(2011)讨论了渗透系数随深度呈指数衰减的情况。实际条件下，含水层空间变异性复杂，尤其是在冲洪积环境下形成的含水层，由于存在大量且随机分布的小型黏质和粉黏质透镜体，含水层非均质性具有随机性和层状结构的特征(Fogg，1986；Deutsch et al., 1989；Koltermann et al., 1996；Lee et al., 2007；Cardenas et al., 2010)。由于很难逐个确定泥岩透镜体的位置和大小，含水层非均质性难以准确刻画，往往造成盆地地下水模拟失真，限制了地下水流系统形成演化规律的认识(张人权等，2005；郝治福等，2006；Zech et al., 2016)。

针对以上问题，本文以鄂尔多斯盆地白垩系地下水流系统为研究实例，选择典型剖面，采用剖面二维数值模拟方法，对比分析均质各向异性与非均质各向异性条件下剖面的地下水流模式，探讨含水层层状非均质对地下水流系统的影响机制，以期深入认识区域地下水流系统形成演化规律。

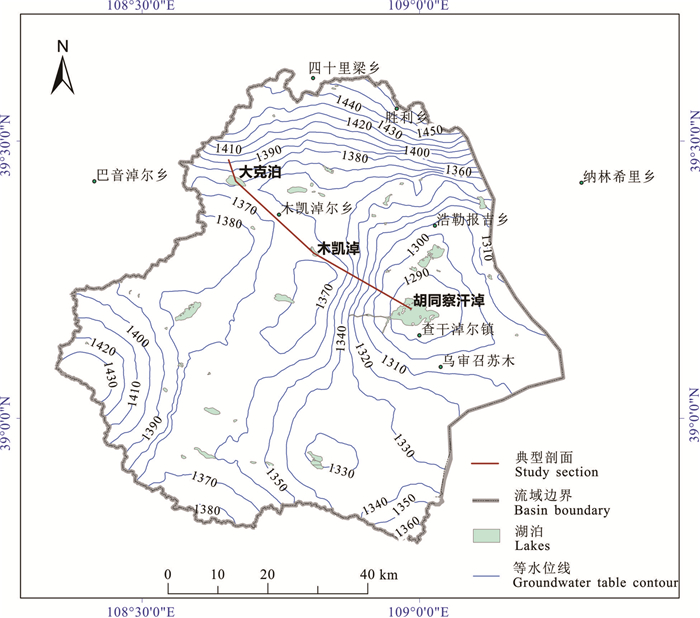
2 研究方法 2.1 研究区概况

鄂尔多斯盆地北部为沙漠高原，地形波状起伏，地下水位与地形起伏一致，地势较高的梁地形成不同级别的地下水分水岭，地势低洼带分布众多湖(淖)，成为地表水和地下水的汇流排泄点，受其控制，发育不同级别地下水流动系统。胡同察汗淖地下水流系统为一个相对独立封闭的内流系统，胡同察汗淖为区域最终排泄点，西部和北部边界为鄂托克梁和四十里梁区域一级地下水分水岭，其他边界为中间和局域水流系统分水岭边界(张二勇等，2012)。含水系统由白垩系洛河组和环河组裂隙孔隙含水层构成，以河流相砂岩为主，呈半胶结状态，孔隙发育，泥质含量较少，沉积韵律不明显，在区域上没有连续的隔水层，总厚度约800 m，底部为侏罗系泥岩隔水层。地下水主要接受大气降水入渗补给，地下水流向受地形控制，由地势较高处向湖淖、河流和低洼地带汇流，最终以蒸发蒸腾方式排泄(图 1)。

2.2 剖面二维数值模型

依托2016—2018年在研究区开展的“鄂尔多斯盆地北部湖泊集中分布区1:5万水文地质调查”项目，通过地下水位统测和动态观测，获取了780组地下水位数据，绘制了研究区地下水等水位线图(图 1)。

沿地下水流动方向布设典型剖面，剖面自西北向东南穿过大克泊、木凯淖两个湖泊排泄点至胡同察汗淖最终排泄基准面，剖面全长约50 km，高程1270~1410 m。在等水位线图上提取剖面地下水位高程，并根据剖面上28组地下水位统测点和8个动态监测点进行校正，得到剖面水位高程值。

2.2.1 边界条件

以白垩系含水层下部侏罗系泥岩隔水层作为模型底部边界，概化为隔水边界；剖面左侧边界为东胜四十里梁地下水分水岭，右侧边界为胡同察汗淖终端排泄点，因此将模型两侧边界概化为零流量边界；由于研究区地下水位受地形控制，且动态监测孔显示地下水位变幅小于3 m，在剖面尺度上可以视为定水头，将剖面上实测的平均地下水位作为模型上部定水头边界，将地下水流模型概化为稳定流模型。剖面二维模型按水平500列，垂向200层剖分，单个网格水平长度100 m，为精细刻画浅部地下水流场，网格垂向剖分自下而上加密。利用GMS中的MODFLOW模块计算，得到剖面地下水位空间分布。采用GMS软件中的MODPATH程序模块，在模型中添加示踪粒子，采用粒子追踪算法生成剖面上的流线分布。

2.2.2 含水层结构和参数

鄂尔多斯盆地北部白垩系保安群环河组和洛河组砂岩，以辫状河流相占绝对优势，中粗粒砂岩分布稳定、厚度巨大、且较均一，构成巨厚的含水统一体，地层结构与岩相分布特征从宏观上控制了白垩系的渗透特征。白垩系内富含泥质夹层，从几厘米到几米厚度不等。泥岩含量在空间上的分布直接控制渗透性的空间分布，而泥质夹层在平面上的延伸长度又决定了白垩系的垂向渗透能力。因此表征泥质夹层的空间分布范围是描述白垩系渗透结构的一项重要内容。由于泥质夹层的发育是局部性和频发性的，很难用确定性方法逐个描述，因此需要用地质统计学方法等效描述泥质夹层空间分布的结构性和随机性。

由于地下水流模拟采用稳定流模型，含水层参数仅设定渗透系数，分均质各向异性和非均质各向异性两种条件赋值。均质情况，渗透系数按研究区渗透系数平均值0.3 m/d统一赋值；含水层各向异性以含水层水平渗透系数和垂向渗透系数的比值以Kh/Kv表示，分别取值为10、50、100、400、700、1000。非均质情况，采用随机模拟方法得到渗透系数平均值为0.3 m/d，且呈对数正态分布的随机场。同时，选用渗透系数方差、水平相关长度以及各向异性值(Kh/Kv)三个变量来表现不同的非均质特征。水平相关长度指渗透系数在水平方向上的相关性，水平相关长度越大，反映含水层的层状非均质性越强，模型中相关长度取值为500、1000、2000、5000、10000、20000 m；渗透系数的方差指渗透系数的离散程度，方差越大说明含水层的非均质程度越高，由于渗透系数采用随机方式生成，模型中方差的取值采用筛选法确定：首先生成任意方差的多组随机场，然后根据生成的随机场中渗透系数的最大值、最小值和频率分布范围是否符合实际条件，筛选接近或符合实际条件的随机场，随机模拟结果表明，方差取值0~2符合实际条件。因此，模型方差从小到大取值为0.13、0.26、0.55、0.65、0.91、1.05、1.26、1.37、1.98；含水层各向异性取值为10、50、100、200、400、700。不同参数条件下，每组模拟共做50次随机模拟，每次随机模拟获得的随机场均进行地下水流模拟。根据流网划分出局部、中间和区域等不同级别水流系统的范围，然后根据不同级别水流系统的垂向发育深度和水平发育规模对比流网结构的差异，以此判断模拟结果的稳定性和代表性。

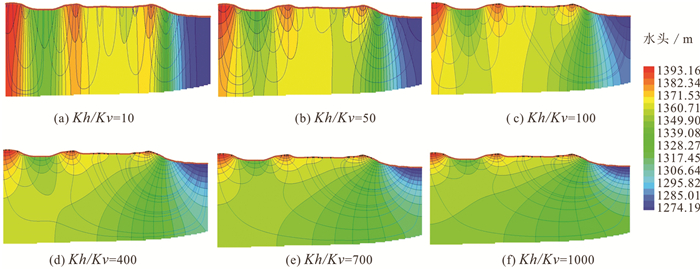
3 结果分析 3.1 均质各向异性条件

当渗透系数K取0.3 m/d，各向异性比值(Kh/Kv)取10、50、100、400、700和1000的剖面地下水流网模拟结果，如图 2所示。随着Kh/Kv的增大，地下水垂向流动受到抑制，而水平流动占据优势，地下水更倾向于水平流动，Kh/Kv对各级水流系统的循环深度具有明显的控制作用。随着Kh/Kv的增加，局部循环变弱，区域循环增加。当Kh/Kv小于100时，地下水垂向流占优，地下水流发育局部(流线由补给区到其相邻排泄区)和中间(流线由补给区到非相邻排泄区)两级水流系统；当Kh/Kv增大至400时，地下水出现了区域流，发育局部、中间和区域(流线由最高补给区到最低排泄区)三级水流系统；当Kh/Kv为700和1000时，可以明显地看出区域循环系统的范围有了明显的增大，局部系统范围减小。

3.2 非均质各向异性条件 3.2.1 渗透系数随机场模拟

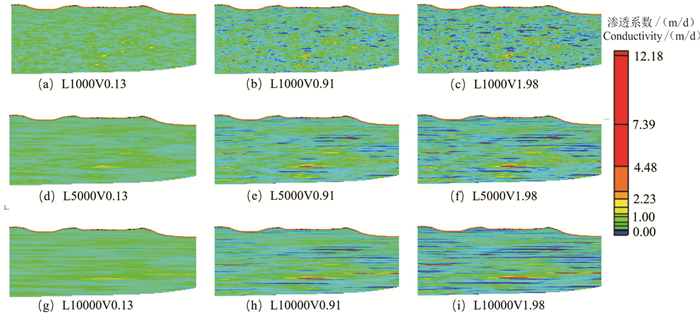
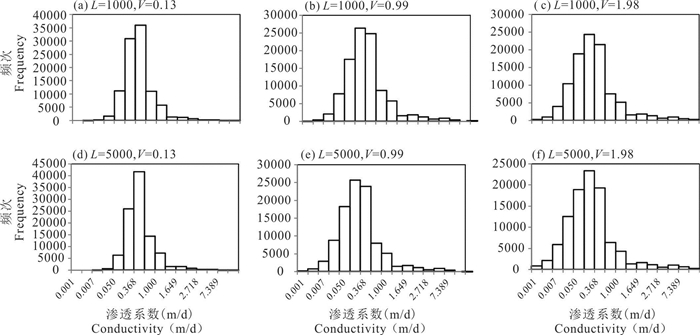
本次采用随机模拟方法生成不同渗透系数方差(V)、水平相关长度(L)以及各向异性比(Kh/Kv)组合的典型随机场324个。选取部分模拟结果进行分析，当水平相关长度为500 m和5000 m，方差分别为0.13、0.91、1.98时的随机场模拟结果如图 3所示，随着方差的增大，含水层的非均质特征明显增强，随着水平相关长度的增加，含水层层状分布特征随之增强。在二者共同作用下，可以很好地表征含水层层状非均质特征的变化规律。对随机模拟得到的渗透系数进行统计分析，得到渗透系数的频率分布直方图(图 4)，可以看出，渗透系数基本满足对数正态分布，且取值范围在0.13~0.36 m/d较为集中。前人根据878个钻孔抽水试验得到的渗透系数值主要集中在0.12~0.4 m/d(侯光才等，2008)。因此，本次随机场模拟的非均质特征可以用来刻画实际条件。

3.2.2 渗透系数方差(V)的影响

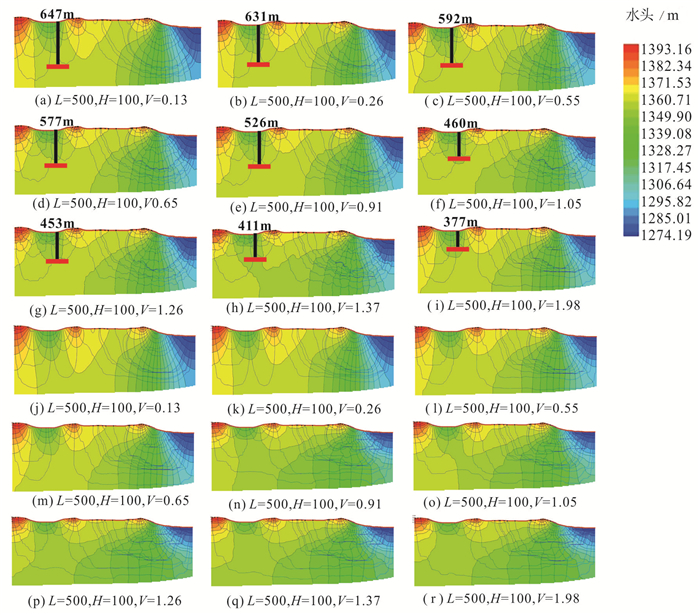
控制渗透系数各向异性及相关长度不变，选取部分模拟结果分析，对比不同方差下的模拟结果(图 5)。当水平相关长度值为500 m和Kh/Kv为100时，随着方差的增大，剖面中流线曲折程度逐渐增加。同时，根据相同位置流线的穿透深度可看出，局部系统的循环深度有逐渐变小的趋势，但地下水仍以垂向流动占优，未出现区域循环系统(图 5a~5i)。与之对比，当水平相关长度为5000时，随着方差的增大，局部系统的循环深度变小的趋势加快，地下水的水平流动开始占优，出现了区域循环系统(图 5j~5r)。上述结果表明，方差增大，含水层渗透系数变异性增大，使得渗透系数小的泥岩透镜体在含水层中出现的次数增加，限制了地下水的水平流动。不同的水平相关长度情况下，即不同泥岩透镜体水平发育长度下，方差对水流系统的影响不同，说明含水层空间变异性对地下水流系统的影响作用受泥岩透镜体长度的影响。

3.2.3 水平方向相关长度(L)的影响

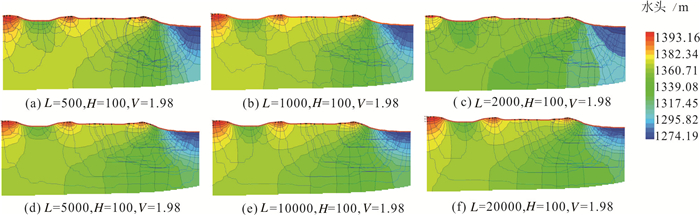
水平相关长度越大表现渗透系数水平方向上的相关性越强，空间上含水介质渗透系数层状分布越明显。选取部分模拟结果进行分析，如图 6所示，当Kh/Kv为100，渗透系数方差为1.98，分别模拟水平相关长度为500、1000、2000、5000、10000、20000 m的情况，可以看出随着水平相关长度的增大，局部地下水的循环深度发生变化，地下水垂向流动受到抑制，水流更倾向于水平流动，当水平相关长度为500 m时，地下水流系统仅发育局部及中间水流系统；当水平相关长度为1000 m时，模型中可见区域水流系统，且随着水平相关长度的增大，区域水流系统的范围逐渐增大。

3.2.4 各向异性比值(H)的影响

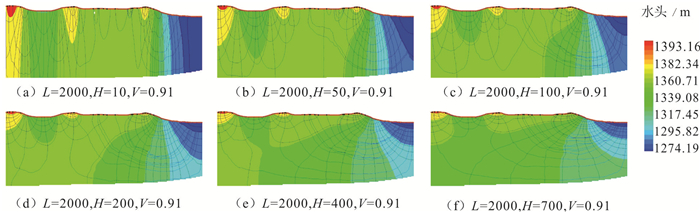
如图 7，为选取水平相关长度为2000，方差为1.98时，改变Kh/Kv为10、50、100、200、400、700时的模拟结果。当Kh/Kv为10时，地下水垂向流占优，局部循环系统占据优势，中间循环微弱，无区域流发育；当Kh/Kv增大到100，可以看到局部、中间、区域三级循环系统发育；Kh/Kv继续增大时，水平流逐渐占优，区域循环系统的范围随之增大。结果表明，非均质条件下Kh/Kv的增加对地下水流系统的控制作用，与均质条件下的规律相同。

非均质条件下Kh/Kv为10时出现中间流动系统(图 7b)，Kh/Kv为100时出现区域流动系统(图 7c)，而均质条件下Kh/Kv达到400时，才出现中间和区域流动系统(图 2c)。方差与水平相关长度可用来刻画白垩系砂岩含水层的层状非均质性。另一方面，非均质条件下Kh/Kv为50、100和400时模拟生成的流网(图 7b、c、e)分别与均质条件下Kh/Kv为100、400和700时的流网(图 6c、e、f)相似。以上结果说明，方差与水平相关长度两个参数共同作用下对水流系统的影响效果与各向异性对水流系统的影响效果一致，采用均质各向异性可以用来等效概化含水层层状非均质性，但会造成等效各向异性值偏大的效应。同时，模拟结果显示，当水平相关长度和方差取值越大时，要生成相似流网，非均质和均质条件模型中Kh/Kv取值差异越大，即等效均质各向异性值越偏大。采用均质各向异性条件等效概化含水层层状非均质性，这是大尺度的地下水流模拟研究常用的处理方法，但这种概化在实际地下水流模拟研究中的确会造成等效各向异性值偏大失真的效应。如前人采用典型剖面数值模拟方法，将鄂尔多斯盆地白垩系含水层概化为等效均质各向异性介质，然后根据分层水头、年龄等约束条件校正得出的Kh/Kv值为700~2000(张俊等，2012；Jiang et al., 2012)。此外，华北平原地下水流模型Kh/Kv取值为10000(Cao et al., 2016)；美国Texas州东部的Wilcox含水层水流模型Kh/Kv取值为10000 (Fogg et al., 1986)。

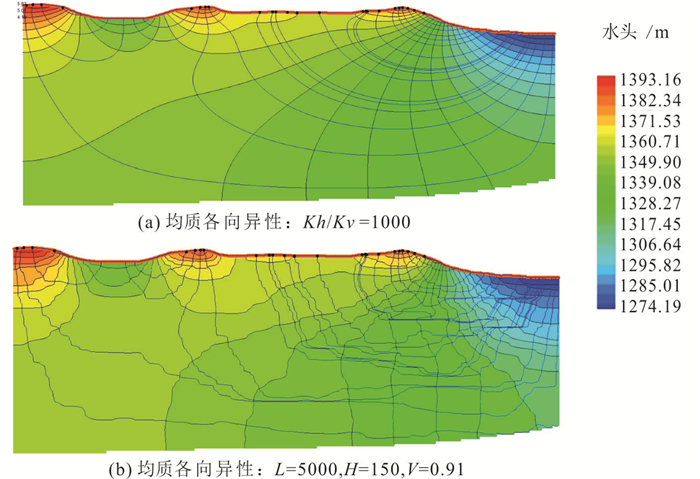
根据前人研究(候光才等，2008)，鄂尔多斯白垩系地下水流系统局部、中间和区域系统的循环深度分别为200 m、400 m和1000 m左右，以此为约束条件，在众多模拟结果中选取与实际条件接近的结果(图 8)。均质条件下，与实际条件较为接近的模拟结果模型Kh/Kv取值为1000时，这与前人研究取值一致。非均质条件下，首先根据白垩系沉积相的空间尺度特征，水平相关长度取值5000 m，根据前人对800余个抽水试验计算获取的渗透系数值统计结果，渗透系数方差取值0.91，然后根据上述约束条件，对Kh/Kv进行调参，当模型模拟结果与实际条件接近时，Kh/Kv取值150。虽然水平相关长度和渗透系数方差的取值只是定性估计，存在不确定性，但大致反映了白垩系含水层的层状非均质特征，这种情况下Kh/Kv的取值也更加接近实际，说明模型的仿真性得到提升，采用以上三个参数来刻画渗透系数随机分布且具有层状结构的方法可以较好地用于仿真模拟。

4 讨论

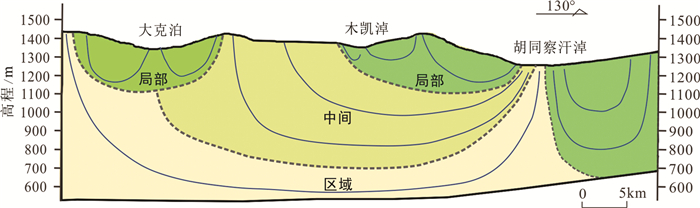
鄂尔多斯盆地北部白垩系地层由早白垩世洛河组、环河组和罗汉洞组构成，以冲积扇相、辨状河相、曲流河相沉积为主，地层岩相主要为粗砂岩、中砂岩，泥岩含量较少，多以透镜体状随机性分布。白垩系含水层厚度大，且无区域性稳定隔水层，各层地下水力联系密切，构成一个具有统一水力联系的巨厚含水体，含水层内地下水可穿层流动，发育了局部、中间和区域多级嵌套水流系统(图 9)，这与Tóth提出的地下水流动模式高度一致(侯光才等，2008；张俊，2014)。

含水层的空间异质性和各向异性是含水层非均质的两个重要方面，二者共同作用影响和控制着区域地下水流模式。鄂尔多斯盆地白垩系地下水流系统各级系统水平规模与垂向深度比值为5000~ 10000，而Toth假设的均质各向同性盆地模型各级系统水平规模与垂向深度的比值为1~2，二者水流系统结构差异巨大。鄂尔多斯盆地白垩系含水层在不同尺度上都存在层状非均质性，实验室尺度上含水层各向异性表现为粉砂、细沙到粗砂的变化，场地尺度上表现为砂岩和泥岩的沉积相旋回。不同尺度上层状非均质的叠加效应，会造成含水层各向异性随研究尺度呈指数增大(Begg，1985；Bethke，1989)，具有明显的尺度效应。由于后期构造活动较弱，白垩系地层产状近似水平，含水层水平和垂向渗透系数存在较大差异，且表现出各向异性的特点。受此影响，地下水垂向流动受到抑制，而水平流动占据优势，地下水更倾向于水平流动，对各级水流系统的循环深度具有明显的控制作用。这是鄂尔多斯盆地地下水流系统结构与Tóth水流模型存在差异的主要原因(张俊等，2012)。

在大尺度地下水流模拟时，当采用均质等效各向异性方法来刻画含水层非均质特征时，很容易导致各向异性值偏大失真的现象，给模型模拟带来巨大的不确定性。同时，由于模拟剖分尺度与含水层参数测量尺度的不匹配，实测参数难以代表模型参数，这进一步加剧了模型的不确定性。本次研究采用随机模拟的方法刻画含水层的非均质性，有助于深入认识随机层状非均质介质对地下水流模式的控制作用，并能较好解释等效均质各向异性偏大的内在原因。但实际上，各向异性参数本身在空间上也表现出很强的空间异质性特点，且具有随机特征(Yeh, et al., 1996)，在水流模型中采用统一参数将其均质化，仍然是一种近似的等效处理手段。

此外，采用与地下水流向基本一致的二维剖面模型进行模拟分析，是地下水流系统理论研究的常用手段(梁杏等，2012；Liang et al., 2013)。但由于三维流的存在，不同深度或不同系统的地下水流方向与剖面方向很难一致，二维模型得到的剖面地下水流场与三维模型可能存在差异(张志远等，2016)，后续研究应该开展三维模型的模拟研究，以检验二维模型取得的规律是否具有普适性。此外，前人对于鄂尔多斯高原的地下水流系统研究为整个鄂尔多斯高原，由于流动系统的循环深度有很强的地段性，且二者模型尺度不同，因此前人得到的不同水流系统循环深度作为本次模拟研究的约束条件存在一定的不确定性。这些问题都给地下水流系统模拟研究带来很大的不确定性。另一方面，地下水流系统是介质场、水动力场、水化学场、温度场等多场统一的有机整体(梁杏等，2012)。因此，后期研究需要用本次研究剖面上的水动力场、化学场及同位素年龄等多种信息的约束(蔡月梅等，2016)，尤其是用分层数据加以校核，开展多学科综合研究方法的多场耦合模拟分析，来有效降低模型的不确定性，从而将地下水流系统的研究从理论研究进一步推向实际。

5 结论

(1) 鄂尔多斯盆地白垩系砂岩含水层不同尺度上层状非均质性的叠加效应，会造成含水层宏观各向异性显著增大，对区域尺度各级地下水流系统的循环深度具有明显的控制作用。

(2) 渗透结构随机模拟的非均质各向异性条件下，采用水平相关长度、渗透系数方差和各向异性值三个变量生成随机场，能很好地刻画区域尺度含水层层状非均质性特征及其对地下水流系统的控制和影响，并能较好解释大尺度地下水流模拟时等效均质各向异性偏大的内在原因。

(3) 大尺度地下水流模拟时，含水层非均质性难移准确刻画，会造成地下水流模型具有很大不确定性。区域地下水流模拟需要水动力场、化学场及同位素年龄等多种约束条件，尤其是分层数据加以校核，并采用多场耦合模拟分析来降低模型的不确定性。